We define a parameterized curve to be any function Z→[a,b]→C where c belongs to the set of complex number.
A parameterized curve is said to be a smooth curve if Z : [a,b]→C is a function such that z(t) is differentiable, and z'(t) is continuous on [a,b] and z't≠0 at any point t.
A piecewise(parameterized) smooth curve is any function Z : [a,b]→C for which there exists a finite number of real numbers a=t0<t₁<....<tn=b such that Z is restricted to each closed interval [ti, ti+1] is parameterized smooth Curves..
A parameterized curve Z : [a,b]→C is said to be closed if z(a)=z(b). It is also said to be closed if Z is not self-intersecting except possibly at its endpoints that is if z(t1)=z(t2),then t1=t2 or t1,t2=a,b.
Methods of parameterizing Curves.
(1) let C be a circle of radius r at a point z0 then C can be parameterized by
 Where z0 is the Centre of the circle. R is the radius of the circle and α and and are the angles from z0 to z1 and z2. So for full circle you use θε[0,2π]. Another important thing to consider is the direction of the contour as θ increases in the above equation, the contour moves round anti-clockwise to make it move in the clockwise direction.
Where z0 is the Centre of the circle. R is the radius of the circle and α and and are the angles from z0 to z1 and z2. So for full circle you use θε[0,2π]. Another important thing to consider is the direction of the contour as θ increases in the above equation, the contour moves round anti-clockwise to make it move in the clockwise direction. 

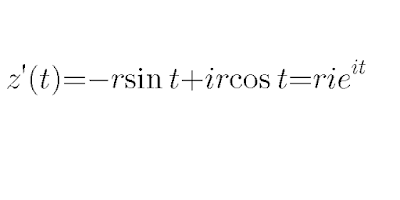






0 Comments
Comments