Determine which of the following are differentiable at 0.
(i)
f(x)=x|x|
(ii)
(i) the differentiability of f(x)=x|x| can be obtained by analyzing the function itself since the function is a product function. First the differentiability of x at 0 exists by using the test of differentiability I.e
So also does the differentiability of |x| at 0 exists by using the test of differentiability. Since the both function are differentiable at 0 when treated as separate functions, then they are also differentiable at 0 when treated as a product function.
f(0.1)=0.2, f(0.01)=0.02, f(0.001)=0.003 which satisfies x>0 but f(x)=0 at x<0 is not differentiable at 0.
(iii) take the derivative of f'(x)




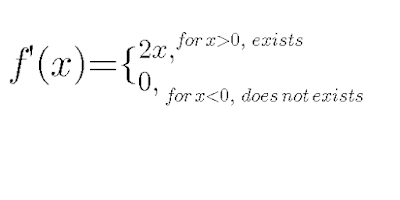







0 Comments
Comments