The mathematics of homomorphism.
In abstract mathematics (algebra), homomorphism can be defined as a map or relation between two algebraic structures of the same type e.g groups, rings or linear spaces. Little wonder it was coined from the greek word "homos" which means "same" and "morphes" which means "shapes".
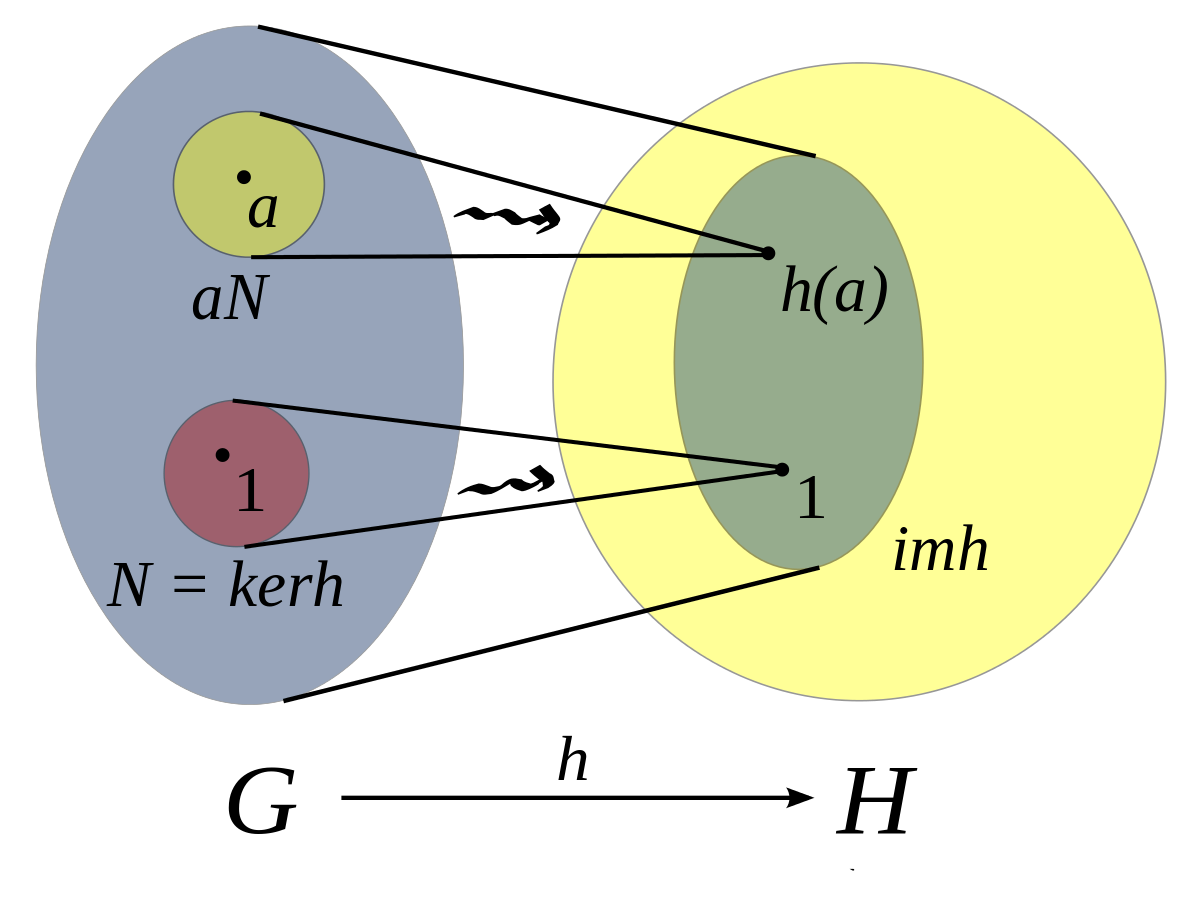
If $A$ and $B$ are two sets of the same algebraic structure defined by a binary operation $.$ then $f:A\rightarrow{B}$ is an homomorphism if $f(x.y)=f(x).f(y)$ for every pair $x,y$ of $A$.
Homomorphisms can also exhibit a property called "operation arity" denoted by the greek letter $\mu$. Which is defined by:
Let $f:A\rightarrow{B}$ be a map that preserves the operation of arity $\mu$ of $k$ defined over $A$ and $B$ then $f(\mu_A(a_1,...,a_k))=$
$\mu_B(f(a_1),...,f(a_k))$ for all $a_1,...,a_k$ in $A$. An example of operation of arity which an homomorphism must satisfy is the $0$-ary operation which are constants.
The major aim of homomorphism is to define a map within the same algebraic structure, thus:
- The semigroup homomorphism is a map between the semigroups which preserves the semigroup operation.
- The monoid homomorphism is a map between the monoids which preserves the monoid operation.
- The group homomorphism is a map between groups that preserves the group operation.
- The ring homomorphism is a map between rings that preserves the ring operation.
- The linear map is an homomorphism of vector spaces that preserves the abelian group structure and scaler multiplication.
- The algebra homomorphism is a map that preserves the algebra operations.
An algebraic structure may have more than one operation, and a homomorphism is required to preserve each operation. Thus a map that preserves only some of the operations is not a homomorphism of the structure, but only a homomorphism of the substructure obtained by considering only the preserved operations e.g a map between monoids that preserves the monoid operation and not the identity element. We also have special homomorphism and there exists more than five examples of special homomorphisms, namely: isomorphism, endomorphism, epimorphism, automorphism, monomorphism.
We will shed more light on them in our upcoming topics.






0 Comments
Comments